Zero-knowledge Proofs on Bitcoin

A zero-knowledge proof enables a prover to validate the truth of a statement without disclosing any information about the underlying inputs. Among the various types of zero-knowledge proofs, zero-knowledge succinct non-interactive arguments of knowledge (zk-SNARKs) represent a significant advancement. These proofs are characterized by their non-interactive nature, compact proof sizes, and efficient verification times.

In recent years, the development of zero-knowledge proofs has led to the emergence of numerous ZKP systems. A particularly promising trend is the integration of ZKP with Bitcoin, which offers a scalable solution for the cryptocurrency. This document aims to introduce our ZKP solution, which leverages BitVM—a relatively mature paradigm in this domain. Our team is actively exploring the future potential of zk-SNARKs. As a member of the BitVM alliance, Bitlayer’s ZKP solution is intricately linked with BitVM. For more detailed information, readers are encouraged to refer to the bitvm website.

Groth16

In 2016, Jens Groth published a groundbreaking paper in which he formalized a proving system that significantly enhanced performance. Notably, for arithmetic circuits, the proofs generated consist of only two elements from the group $G_1$ and one element from the group $G_2$. Here, $G_1$ and $G_2$ refer to two torsion groups within the context of pairing in Elliptic Curve Groups.

Due to its succinctness, the Groth16 proof has emerged as one of the most efficient and widely adopted solutions in the blockchain ecosystem, where resources on the main chain are extremely limited. Many Ethereum rollups prefer to utilize Groth16 for verification on Layer 1 (L1). Additionally, ZKVM projects such as Risc0 and SP1 incorporate Groth16 as the final recursive circuit. The Groth16 proof has been validated through numerous use cases, showcasing its robustness and versatility in practical applications.

How Groth16 is Applied to Bitcoin?

Like many other zk-SNARKs, Groth16 adheres to the same standard definition. It involves three algorithms, where $x$ is a public statement, $w$ is a witness, and a binary relation $(x,w) \in R$ holds.

• $(pk, vk) \leftarrow \text{setup}(R)$: The setup procedure produces two public parameters $pk$ and $vk$. Here, $pk$ is a common reference string that defines the statement $x$, while $vk$ serves as a trapdoor for the relation $R$.
• $\pi \leftarrow \text{prove}(R, pk, x, w)$: The prover takes the common reference string $pk$ and some $(x, w) \in R$ and returns an argument $\pi$ for that relation.
• $0/1 \leftarrow \text{verify}(R, pk, x, \pi)$: The verifier either rejects (0) or accepts (1) the given argument $\pi$. For the completeness of Groth16, this algorithm will return 1 if $(x, w) \in R$ is satisfied.

One native way to scale Bitcoin is by proving off-chain and verifying on-chain. One of the main challenges with this approach is that the $\text{verify}$ algorithm is too large to execute within a Bitcoin transaction. However, thanks to the optimistic computation paradigm of BitVM, the verification process can be split into manageable chunks, allowing the challenger to select one of these segments.

Despite this chunking method, the intermediate values of these segments need to be committed by the operator, which can still be substantial within the Bitcoin execution environment. Therefore, even with chunking, optimization of the $\text{verify}$ algorithm is crucial for practical implementation.

This article will delve into the specifics of Groth16. First, some primary concepts and symbols will be quickly reviewed to align with the readers. Then, a key optimization related to verifying pairing will be introduced. Finally, the discussion will guide readers through the core idea of chunking the $\text{verify}$ algorithm. By the end, readers will gain an in-depth understanding of zero-knowledge proofs in BitVM.

Elliptic Curve Group

The Elliptic Curve Group (ECG) is widely used due to its efficiency compared to finite fields under large primes. In this context, the BN254 elliptic curve group is selected for both security and efficiency. The BN254 curve $C(F_{q^k})$ is defined by the equation $C: y^2 = x^3 + 3$, based on a finite field $F_{q^k}$, where $q$ is an efficiently chosen large prime.

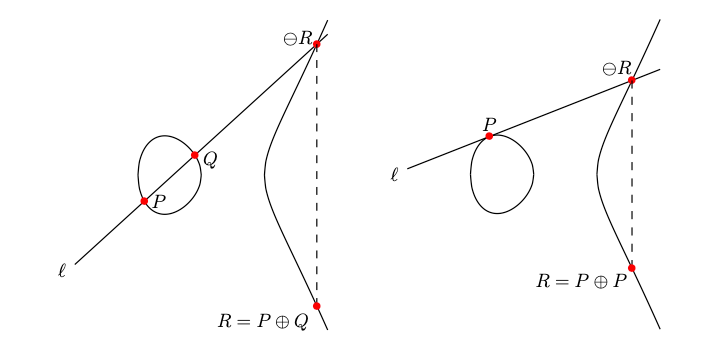
The ECG of BN254 is defined by divisors, and we introduce a point in projective space known as the point at infinity $\mathbb{O}$. The points on BN254, along with $\mathbb{O}$, form a group that adheres to the chord-and-tangent rule. The figure below illustrates two cases of the chord-and-tangent rule:

• $R = P \oplus Q$, which represents the addition of two distinct points.
• $R = P \oplus P$, which represents the doubling of a single point.
• $P = P \oplus \mathbb{O}$ and $\mathbb{O} = \mathbb{O} \oplus \mathbb{O}$, which demonstrate the rules governing the point at infinity.

Pairing Computation

Selecting an efficient pairing is a common method to reduce verification time. For the pairing in the BN254 elliptic curve group (ECG), two torsion groups are specifically chosen, both based on a smaller finite field with characteristic $q$. Following the standard notation for pairings, we denote $G_1$ as $C(F_q)$, $G_2$ as $C(F_{q^2})$, and $G_T$ as $C(F_{q^k})$.

The ate pairing on $r$-torsion groups is defined as a map

$e: G_1 \times G_2 \rightarrow G_T$ and is expressed as $e(P, Q) = f_{r, Q}^{(q^k-1)/r}(P)$ where $P \in G_1$, $Q \in G_2$, $k$ is the embedding degree, and $f_{r, Q}$ is a function whose divisor is $r(Q) - r(\mathbb{O})$. It is important to note that this is an optimized and reduced version. The computation of the Tate pairing in the BN254 ECG can be further simplified through algebraic optimization.

By choosing any $r$ such that $\gcd(r, t) = 1$, for $rQ = \mathbb{O}$, we have

$f_{tr, Q}(P) \rightarrow f_{r, Q}(P)^t \cdot f_{t, rQ}(P) \rightarrow f_{r, Q}(P)^t,$ which shows that $f_{tr, Q}$ is a valid substitution for $f_{r, Q}$. In the BN254 ECG setting, $tr = 6x + 2 + q - q^2 + q^3$, where $x = 4965661367192848881$. The evaluation of $f_{tr, P}$ is more efficient to compute by leveraging the Frobenius map. A similar technique is also applied during the verification of the pairing, rather than through direct computation.

Groth16 Verifier

The Groth16 verifier utilizes the properties of pairings while acknowledging its inherent inefficiencies. The proof is defined as $\pi = ([A]_{1}, [C]_{1}, [B]_{2}) \in G_1^2 \times G_2,$

and the verifier accepts the proof if and only if the following condition holds:

$[A]_{1} \cdot [B]_{2} = [\alpha]_{1} \cdot [\beta]_{2} + \sum_{i = 0}^l z_i \left[(\beta A_i(\tau) + \alpha B_i(\tau) + C_i(\tau)) \cdot \gamma^{-1} \right] \cdot [\gamma]_{2} + [C]_{1} \cdot [\delta]_{2},$

where $\alpha, \beta, \tau, \gamma, A_i, B_i, C_i$ are precomputed during the setup phase, $l$ is the number of public inputs, and $z_i$s are the public inputs.

This equation can be simplified to the following form, which outlines the two phases of the Groth16 verifier:

1. Multiple scalar multiplications with fixed points.
2. Four pairs of pairing computations, where three of them involve fixed points, and one does not.

The simplified equation is given by: $e([A]_{1}, [B]_{2}) = e([\alpha]_{1}, [\beta]_{2}) \cdot e\left(\sum_{i = 0}^l z_i \sigma_i, [\gamma]_{2}\right) \cdot e([C]_{1}, [\delta]_{2}).$

Optimization on Verifying Pairing

In the context of zk-SNARKs, the process of pairing computation provides us with an opportunity for pre-computation rather than direct pairing calculations. This article will present two main optimization strategies. We encourage readers to refer to the original ideas outlined in the paper On Proving Pairing, though it is important to note that this paper does not fully encompass the implementation details of BitVM.

The first optimization demonstrates that the final exponentiation of ${q^k-1}/{r}$ can be viewed as a reduction to the equivalence class of $F^*_{q^k} / (F^*_{q^k})^r$. If we can identify a pre-computed $c \in F^*_{q^k}$ and verify that the result of the pairing is equal to $c^\lambda$, where $\lambda$ is a multiple of $r$ that can be computed efficiently, this process will significantly enhance efficiency.

The second optimization indicates that the coefficients of each line in the Miller loop can be pre-computed. In the context of Groth16, the chord line and vertical line for the three fixed-point pairs are always constant. For the non-fixed-point pair, the chord line and vertical line can be verified at runtime.

Below, we outline the algorithm used by BitVM, which corrects errors found in the original paper. In the following description, $\mathcal{T}$ represents all pre-computed lines that have been carefully selected for use. The index of pairs with non-fixed points is denoted by $b$.

$$\begin{align*} \textbf{Input } & (P_i, Q_i) \text{where } i \in \{0..3\}, c \in F_{q^k}, w \in F_{q^3}, \text{all } \text{precomputed } \text{lines } \mathcal{T}. \\ \textbf{Output } & \text{1 } \text{where } \Pi_{i=0}^3 e(P_i, Q_i) = 1, \text{otherwise } 0. \\ \textbf{Algorithm } & \text{} \\ 1. \space & \text{represent } s = 6x + 2 = \textstyle\sum\nolimits_{i=0}^L{s_i2^i} \text{ where } s_i \in \{-1, 0, 1\} \\ 2. \space & T \leftarrow Q_b \\ 3. \space & \text{compute } c^{-1} \text{ by } c \\ 4. \space & f \leftarrow c^{-1} \\ 5. \space & \textbf{For } i = L-2 \textbf{ to } 0 \\ 6. \space & \quad f \leftarrow f^2 \\ 7. \space & \quad f \leftarrow f\cdot l_i.\text{evaluate}(P_i) \text{ For } i \in \{0..3\} \text{ where } l_i \text{ is } \text{chosen } \text{from } \mathcal{T} \\ 8. \space & \quad \textbf{assert } l_b.\text{isTagent}(T) \\ 9. \space & \quad T = l_b.\text{double}(T) \\ 10. \space & \quad \textbf{If } s_i = 1 \textbf{ then} \\ 11. \space & \quad \quad f \leftarrow f \cdot c \\ 12. \space & \quad \quad f \leftarrow f\cdot l_i.\text{evaluate}(P_i) \text{ For } i \in \{0..3\} \text{ where } l_i \text{ is } \text{chosen } \text{from } \mathcal{T} \\ 13. \space & \quad \quad \textbf{assert } l_b.\text{isLine}(T, Q_b) \\ 14. \space & \quad \quad T = l_b.\text{add}(T, Q_b) \\ 15. \space & \quad \textbf{End } \textbf{If} \\ 16. \space & \quad \textbf{If } s_i = -1 \textbf{ then} \\ 17. \space & \quad \quad f \leftarrow f \cdot c^{-1} \\ 18. \space & \quad \quad f \leftarrow f\cdot l_i.\text{evaluate}(P_i) \text{ For } i \in \{0..3\} \text{ where } l_i \text{ is } \text{chosen } \text{from } \mathcal{T} \\ 19. \space & \quad \quad \textbf{assert } l_b.\text{isLine}(T, -Q_b) \\ 20. \space & \quad \quad T = l_b.\text{add}(T, -Q_b) \\ 21. \space & \quad \textbf{End } \textbf{If} \\ 22. \space & \textbf{End } \textbf{For} \\ 23. \space & f \leftarrow f \cdot w\\ 24. \space & f \leftarrow f \cdot (c^{-1})^q \cdot c^{q^2} \cdot (c^{-1})^{q^3} \\ 25. \space & f \leftarrow f\cdot l_i.\text{evaluate}(P_i) \text{ For } i \in \{0..3\} \text{ where } l_i \text{ is } \text{chosen } \text{from } \mathcal{T} \\ 26. \space & f \leftarrow f\cdot l_i'.\text{evaluate}(P_i) \text{ For } i \in \{0..3\} \text{ where } l_i' \text{ is } \text{chosen } \text{from } \mathcal{T} \\ 27. \space & f \leftarrow f\cdot l_i''.\text{evaluate}(P_i) \text{ For } i \in \{0..3\} \text{ where } l_i'' \text{ is } \text{chosen } \text{from } \mathcal{T} \\ 28. \space & Q_1 \leftarrow \pi(Q_b), Q_2 \leftarrow \pi(Q_1), Q_3 \leftarrow \pi(Q_2) \text{ where } \pi \text{ is } \text{Frobenius } \text{map } \\ 29. \space & \textbf{assert } l_b.\text{isLine}(T, Q_1) \\ 30. \space & \textbf{assert } l_b'.\text{isLine}(T, -Q_2) \\ 31. \space & \textbf{assert } l_b''.\text{isLine}(T, Q_3) \\ 32. \space & \textbf{Return } f \end{align*}$$